一、算术平均数

1.算术平均数（Arithmetic Mean）是一组数值的总和除以数值的个数。它是最直观、最常用的平均数类型。计算公式如下：

其中：
（1）xˉ表示算术平均数；
（2）xi 表示第 i 个数据点；
（3）n 表示数据的总数。
2.示例：
假设某班级有5名学生的数学成绩分别为80、85、90、95、100，则该班级学生的数学成绩算术平均数为：
xˉ=580+85+90+95+100=90
3.特点
（1）简单易懂：计算方法直观，易于理解和应用。
（2）广泛应用：适用于大多数数值型数据，尤其在数据分布对称或无明显极端值时，能较好地代表数据集的中心位置。
（3）对极端值敏感：极端值（异常大或异常小的数值）会显著影响算术平均数的值，使其偏离大多数数据的实际水平。
4.应用场景
（1）经济分析：计算平均工资、平均物价指数等。
（2）教育研究：评估学生的平均成绩、平均学习时间等。
（3）市场分析：分析平均销售额、平均市场份额等。

二、几何平均数

1.几何平均数（Geometric Mean）是一组正数数值的连乘积的 n 次方根。它常用于计算平均增长率、平均比率等。计算公式如下：

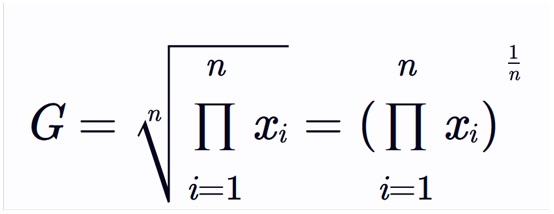
其中：
（1）G 表示几何平均数；
（2）xi 表示第 i 个正数数据点；
（3）n 表示数据的总数。
2.示例：
假设某投资项目的年回报率分别为10%、15%、20%，则该项目的平均年回报率为几何平均数：

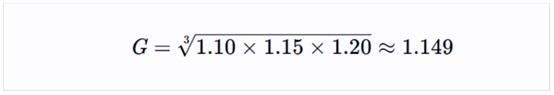
即平均年回报率约为14.9%。
3.特点
（1）适用于比率数据：特别适用于计算平均增长率、平均比率等，能够反映数据在一段时间内的平均变化率。
（2）对极端值不敏感：由于计算的是连乘积的 n 次方根，极端值对几何平均数的影响相对较小。
（3）计算相对复杂：需要计算连乘积和开方，计算过程相对复杂一些。
4.应用场景
（1）金融投资：计算平均收益率、平均增长率等，评估投资项目的长期表现。
（2）生物学研究：计算生物种群的平均增长率，了解种群数量的变化趋势。
（3）经济学分析：分析经济增长率、通货膨胀率等，评估经济指标的平均变化水平。

三、总结：算术平均数VS几何平均数