在统计分析中，衡量两个变量之间的相关性是一个重要任务。皮尔逊积矩相关系数和斯皮尔曼等级相关系数是两种常用的方法，用于衡量变量之间的相关性。皮尔逊相关系数适用于线性关系且数据服从正态分布的情况，而斯皮尔曼等级相关系数则更适用于非线性关系或数据不服从正态分布的情况。

一、皮尔逊积矩相关系数

离散数据是指其数值只能用自然数或整数单位计算的数据，其数值是间断的，相邻两个数值之间不再有其他数值。简单来说，离散数据是可以通过计数得到的数据，通常是一些独立的、不连续的点。例如，班级中学生的人数、企业员工的数量、抛硬币正面朝上的次数等，这些数据只能取整数值，不能取小数或其他非整数值。与离散数据相对的是连续数据，连续数据可以在一定区间内取任意实数值，如人的身高、体重、温度等。
皮尔逊积矩相关系数，简称皮尔逊相关系数，是衡量两个连续变量之间线性关系强度和方向的统计指标。
（一）取值范围：
皮尔逊相关系数的取值范围为 [−1,1]。
当相关系数为 1 时，表示两个变量完全正相关，即一个变量增加时，另一个变量也增加。
当相关系数为 −1 时，表示两个变量完全负相关，即一个变量增加时，另一个变量减少。
当相关系数为 0 时，表示两个变量之间无线性相关关系。
（二）计算公式：
皮尔逊相关系数 r 的计算公式为：

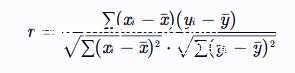
其中，xi 和 yi 分别是两个变量的观测值，x（拔）和 yˉ（拔）分别是两个变量的均值。
皮尔逊相关系数只能衡量两个变量之间的线性关系；对数据的要求较高，需要变量服从或接近正态分布。

（三）适用场景
皮尔逊相关系数适用于衡量两个连续变量之间的线性关系。在社会科学研究中，可用于分析教育水平与收入的关系，或年龄与消费习惯的关联；在自然科学实验中，可用于探究环境温度与化学反应速率的相关性。
（四）假设条件
1.变量类型：两个变量应为连续型数据。
2.线性关系：两个变量之间存在线性关系。
3.正态分布：两个变量大致符合正态分布。
4.数据配对：数据集中每个观测数据包括成对数据。
5.无异常值：数据集中不应包括极端异常值。

二、斯皮尔曼等级相关系数

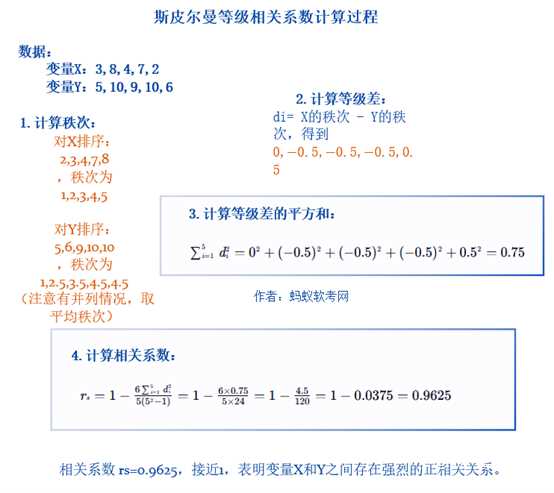
斯皮尔曼等级相关系数，简称斯皮尔曼相关系数，是一种非参数统计量，用于衡量两个变量的等级之间的关联程度。它基于变量的秩次（排序后的位置）进行计算，不依赖于数据的分布形态，能有效处理非线性关系和非数值型的有序数据。斯皮尔曼相关系数的取值范围也在-1到1之间，绝对值越接近1表示等级关联越强，0则表示不存在等级相关关系。
（一）计算公式：

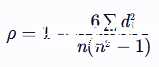
其中，di 是两个变量排序后的等级差，n 是观测值的数量。

（二）适用场景：
1.数据为定序数据：如比赛名次、成绩等级、满意度排序等。
2.数据分布未知或不满足正态分布：当无法确定数据是否服从正态分布，或者明确知道数据不服从正态分布时。
3.变量间为非线性关系：只要两个变量之间存在单调变化趋势（不一定是线性），都可以用它来衡量相关性。
（三）假设条件：
1.数据类型：适用于两列等级变量或由连续变量转化而来的等级数据。
2.分布无关性：不要求变量服从正态分布，也不要求样本量足够大。